A Framework to Quantify Approximate Simulation on Graph Data

Abstract

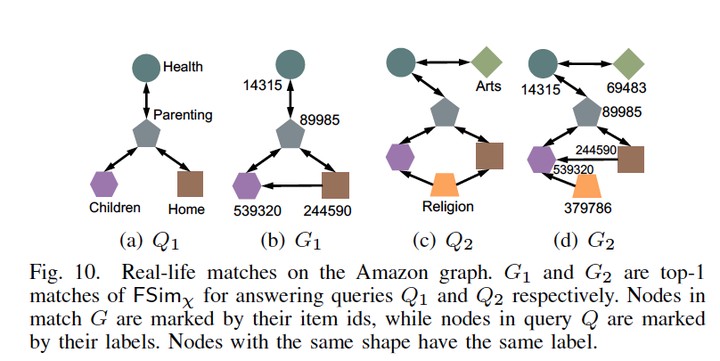
Simulation and its variants (e.g., bisimulation and degree-preserving simulation) are useful in a wide spectrum of applications. However, all simulation variants are coarse “yes-or-no” indicators that simply confirm or refute whether one node simulates another, which limits the scope and power of their utility. Therefore, it is meaningful to develop a fractional $\chi$-simulation measure to quantify the degree to which one node simulates another by the simulation variant $\chi$. To this end, we first present several properties necessary for a fractional $\chi$-simulation measure. Then, we present FSim$_\chi$, a general fractional $\chi$-simulation computation framework that can be configured to quantify the extent of all $\chi$-simulations. Comprehensive experiments and real-world case studies show the measure to be effective and the computation framework to be efficient.