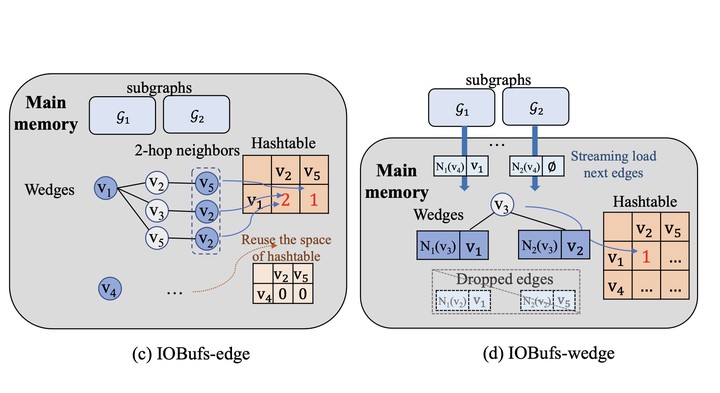
Abstract
Butterfly (a cyclic graph motif) counting is a fundamental task with many applications in graph analysis, which aims at computing the number of butterflies in a large graph. With the rapid growth of graph data, it is more and more challenging to do butterfly counting due to the super-linear computation complexity and large memory consumption. In this paper, we study I/O-efficient algorithms for doing butterfly counting on hierarchical memory. Existing algorithms of the kind cannot guarantee I/O optimality. Observing that in order to count butterflies, it suffices to ``witness” a subgraph instead of the whole structure, a new class of algorithm called semi-witnessing algorithm is proposed. We prove that a semi-witnessing algorithm is not restricted by the lower bound $\Omega(\frac{|E|^2}{MB})$ of a witnessing algorithm, and give a new bound of $\Omega(\min(\frac{|E|^2}{MB}, \frac{|E||V|}{\sqrt{M}B}))$. We further develop the IOBufs algorithm that manages to approach the I/O lower bound, and thus claim its optimality. Finally, we make effort to parallelize IOBufs to further improve the performance and scalability. We show in the experiment that IOBufs significantly outperforms the state-of-the-art algorithms EMRC and BFC-EM. In addition, it can scale to graphs of billions of edges even when configuring a small memory (e.g. 10% of the graph size).